Java Applet on Additive Decomposition

Java Applet on Additive Decomposition

Start the applet

INTRODUCTION

Applet demonstrates additive decomposition, wherein the graph of the FSM is partitioned into node disjoint subsets. The network of interacting sub-FSMs corresponds to a given partition on the set of states of source FSM. The network of FSMs consists of components working alternatively in time, i.e. all components except one are suspended in one of extra state (the “wait” state). This property gives opportunity to apply sleep mode operation (dynamic power management) for saving power consumption.

SHORT THEORETICAL BASICS

Prototype FSM model

Formally, FSM is a quintuple < S, X, Y, , > where

S = { s1, … , sn } is a set of states;

X = { x1, … , xl } is a set of primary input variables;

Y = { y1, … , ym } is a set of primary output variables;

: D() S is a multiple valued next state function with
domain D () ={0, 1} l S and codomain S ;
{0, 1} represents a set of values (symbols) each input variable xi may assume;

: D() R() is an output function with
domain D() = {0, 1} l S and codomain R() ={0, 1}m ;
{0, 1} is a set of values each output variable yi may assume.

Example Prototype FSM

S= { s1 , s2 , … , s8 }

X= { x1, x2 , … , x8 }

Y= { y1 , y2 , … , y14 }

FSM description

Decomposition procedures

Generation of the initial partition
Definition of states in component FSMs
Definition of the set of external input variables of component FSM
Generation of the set of the set of internal (additional) input variables
Definition of the set of output variables of component FSMs
Generation of transition and output functions of component FSMs
Realization of FSM network.

Partitions

The set of states of (component) sub-FSM

Define set of states in component automata as:

where:
Bm- is the block of the partition ,
am - is the additional state that exists in each component automata.

Let define states of component automata in our example:

S={ s1 , s2 , … , s8 }
={ { s1, s4, s7 }, { s2 , s3, s6 }, { s5 , s8 } }

S1 = { s1, s4, s7, a1 }
S2 = { s2, s3, s6, a2 }
S3 = { s5, s8, a3 }

Set of external input variables

X(Bm) is the set of external input variables at all transitions from the states of block Bm in the transition table of the prototype FSM A:

In our example:
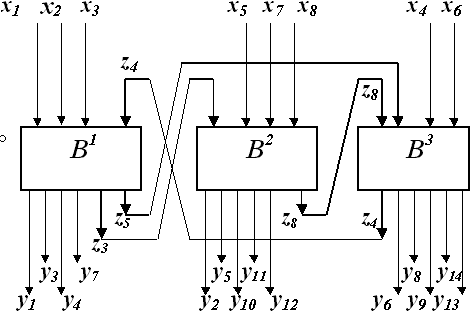
X(B1) = { x1, x2, x3 }
X(B2) = { x5, x7, x8 }
X(B3) = { x4, x6 }

={ { s1, s4, s7 }, { s2 , s3, s6 }, { s5 , s8 } }

Set of external output variables

Y(Bm) is the set of external output variables at all transitions from the states of block Bm in the transition table of the FSM A:

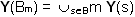
In our example:
Y(B1) = { y3, y4, y7 }
Y(B2) = { y2, y5, y10, y11, y12 }
Y(B3) = { y6, y8, y9, y13, y14 }

Example FSM parameters

Component FSMs B2 and B3

FSM Network

Additional theory is available here or here
APPLET MANUAL

LIST OF PUBLICATIONS:

WARNING: This page contains links to PDF files of articles that may be covered by copyright. You may browse the articles at your convenience. (in the same spirit as you may read a journal or a proceeding article in a public library). Retrieving, copying, or distributing these files, however, may violate the copyright protection law. We recommend that the user abides international law in accessing this directory.

M. Kruus, H. Lensen, and A. Sudnitson, “Web-Based Tools for Decomposition-Oriented Digital Design”, in Proc. 1st International Congress on Mechanical and Electrical Engineering and Technology (MEET/MARIND’2002), Varna, Bulgaria, 2002, v.1, pp. 261-266. (ISBN: 954-20-0211-4)

S. Devadze, M. Kruus, and A. Sudnitson, “Web-Based Software Implementation of Finite State Machine Decomposition for Design and Education”, in Proc. International Conference on Computer Systems and Technologies (CompSysTech’2001), Sofia, Bulgaria, 2001, v.4, pp. 1-7. (ISBN: 954-9641-25-2)

A. Jutman, M. Kruus, A. Sudnitson, and R. Ubar “Distance-Learning Tools for Digital Design and Test Issues”, in Proc. 29th International Conference on Information Technologies in Science, Education, Telecommunication, Business (IT+SE’ 2002), Gurzuf, Ukraine, 2002, pp.269-272.

S. Devadze, E. Fomina, M. Kruus, and A. Sudnitson, “Web-Based System for Sequential Machines Decomposition”, in Proc. IEEE EUROCON 2003 International Conference on Computer as a Tool, Ljubljana, Slovenia, 2003, V. 1, pp. 57-61. (ISBN: 0-7803-7763-X, IEEE Catalog No.: 03EX665)

Last update: 3 August, 2004