2. ABSTRACT AUTOMATA
 

2.1. Definition

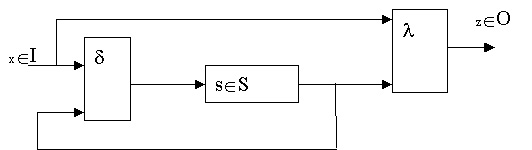
Def. A Mealy type automaton is a quintuple  where

• I is a finite nonempty set of inputs
• S is a finite nonempty set of states
• O is a finite nonempty set of outputs
• : S  I S is the transition function
• : S  I O is the output function

Moore automaton	State automaton	Autonomous automaton or o´clock	Primitive automaton or combinatorial circuit
: S  I S : SO	A=(I,S,) : S  I S	A=(S,O,,) : S x I S : Sx IO	A=(I,O,) : IO

2.2. Subautomaton

Def. An automaton  is a subautomaton of the automaton if and only if

2.3. Isomorphism

Def. Two automata  and  are isomorphic if and only if there exist three one-to-one onto mappings

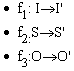such that

and 

2.4. Homomorphism

Def. An automaton  is a homomorphic image of the automaton  if and only if there exists three onto mappings

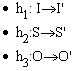such that

Example of homomorphism

2.5. Equivalence

Def. If and  are two Mealy (Moore) automata, then the states  and  are said to be equivalent iff  for all .
NB! A₁=A₂ - equivalence relation on the set of states

2.5.1. Lemma: Equivalent states s₁ and s₂ of automata A₁ and A₂ go into equivalent states under each input.  

2.5.2. Equivalence of automata

Def. Two automata are equivalent if s₁ÎS₁ has an equivalent state  and each  has an equivalent state .

2.5.3. Reduced automaton

Def. An automaton A is reduced if s₁ equivalent to s₂ implies that s₁=s₂.

2.5.4. Realization

Def. An automaton A' is said to be a realization of automaton A if there exists a subautomaton of A' which is isomorphic (homomorphic) to A.

Last update: 3 August, 2004