3. ABSTRACT NETWORK

3.1. Definition

Def. An automata network  consists of

1. I - input alphabet of N
2. - a set of component automata
• I_i' - internal input alphabet
• I_i'' - external input alphabet;
3. O- output alphabet of N;
4. - a set of connection functions of component automata;
5. - a set of input functions;
6. - output function of N.

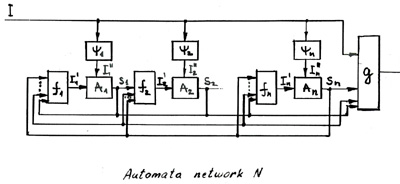
3.3. Automaton defined by network

Def. Automata network N defines the resulting automaton A_N:

3.4. Realization of automaton  

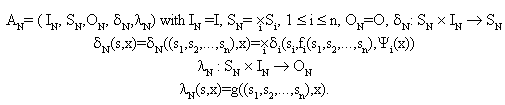
Def.An automaton A' is said to be a realization of automaton A iff there exists a subautomaton of A' which is isomorphic to A.

3.5. Decomposition for given automaton

Def. Automata network N is a decomposition for given automaton A iff A_N is a realization of A.

Let , , be a partition on the set of states of automaton .

3.6. Main theorem of decomposition

Theorem Given an automaton  and a set of partitions , ; then there exists a network N which is a decomposition of A if and only if .

Last update: 3 August, 2004