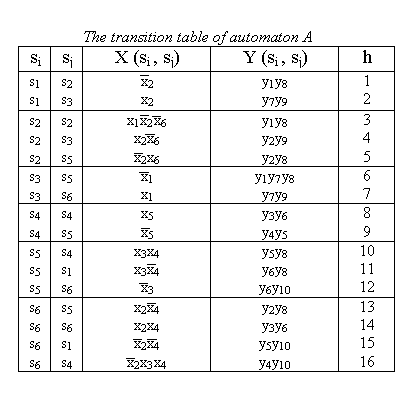
7. ADDITIVE DECOMPOSITION

7.1. Initial Automaton

Assume that we are given a Mealy type automaton  and the partition. To illustrate each step of decomposition with an example, we will use some defined automaton A, and partition 

B¹ = {1, 2, 3};  B² = {4, 5, 6}

Let put network N  with n component automata in accordance to pair. The number of component automata is equal to the number of blocks in the partition .
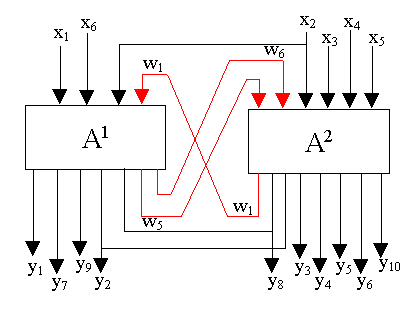
So, in our example there will be two component automata A¹ and A², since there are two blocks (B¹ and B²) in the partition .
 

7.2.  Definition of States in Component Automata

First, define set of states in component automata as:

Let define states of component automata in our example:
C¹ = (s₁, s₂, s₃, c₁}
C² = {s₄, s₅, s₆, c₂}
 

7.3. Set of Input and Output Variables

To define inputs and outputs of component automaton let put sets X(B^m), Y(B^m), G^m, T^m, Q^m in accordance to each block of the partition :

• X (B^m) is the set of input variables at all transitions from the states of block B^m in the transition table of the automaton A:

In our example:
X(B¹) = {x₁, x₂, x₆}
X(B²) = {x₂, x₃, x₄, x₅}
 
• Y(B^m) is the set of output variables at all transitions from the states of block B^m in the transition table of the automaton A:

 
In our example:
Y(B¹) = (y_1, y₂, y₇, y₈, y₉}
Y(B²) = {y₂, y₃, y₄, y₅, y₆, y₈, y₁₀}
 
• G^m is the set of states not included in B^m, from which there are transitions to the states of B^m:

 
In our example:
G¹ = {s₅, s₆}
G² = {s₂, s₃}
 
• T^m is the of states not included in B^m, to which there are transitions from the states of B^m:

In our example:
T¹ = {s₅, s₆}
T² = {s₁}
 
• Q^m is the subset of states of Bm, to which there transitions from states not included in B^m (from states of G^m):

 
In our exmple:
Q¹ = {s₁}
Q² = {s₅, s₆}

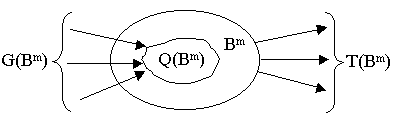
Now we can define the set of input vaiables X^m:

Here  is the set of additional input variables which connect other component automata with this automaton A^m. To define  let put the additional input variable w_k in accordance to each state in set Q^m.  So, the number of elements in  is equal to the number of states in Q^m:

In our example:
{w₁}
{w₅, w₆}

Similarly, we define the set of output variables Y^m:

Here  is the set of additional output variables which connect the automaton Am with other component automata. To define  let put the additional output variable w_i in accordance to each state in set T^m. So, the number of elements in is equal to the number of states in T^m:

In our example:
{w₅, w₆}
{w₁}

In other words states Q^m and T^m define the sets of additional input ()  and output ():
if  then  and
if  then

7.4. Definition of Transition and Output Functions

Let

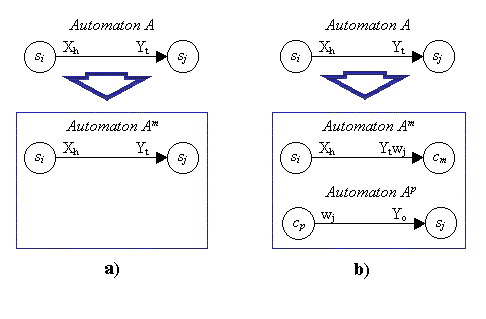
a) If (s_i and s_j are states of the same component automaton A^m), then

is the transition in component automaton A^m

b) If  (s_i and s_j are states of two different component automata A^m and A^p ). Then, the component automaton A^m transits from state s_i to the additional state c_m with the output Y_t and additional output w_j :

The additional output  w_j of the component automaton A^m is the input of the component automaton A^p . This input w_j produces the transition from the additional state c_p to the state s_j with the output Y₀ in the automaton A^p :

How transitions in automaton A are defined in component automata showed on the figure below:

7.5. Reduced Procedure of Decomposition

The procedure of decomposition can be reduced to:

a) copiying row s_i, s_j , X(s_i, s_j), Y(s_i, s_j) from the table of the automaton A to the table of component automaton A^m , if s_i and s_j are the states of A^m.
b) the replacement of the row  s_i, s_j,X(s_i, s_j), Y(s_i, s_j) in the table of automaton A by the row  s_i, c_m X(s_i, s_j) Y(s_i, s_j)w_i in the table of component automaton A^m and the row c_p , a_j , w_j in the table of component automaton A^p, s_i is the state of A^m and s_j is the state of A^p; mp.
c) adding row c_m, c_m to the transition table of component automaton A^m.

As result of decomposition of our sample automaton A we obtain the network N with two component automata A¹ and A² :

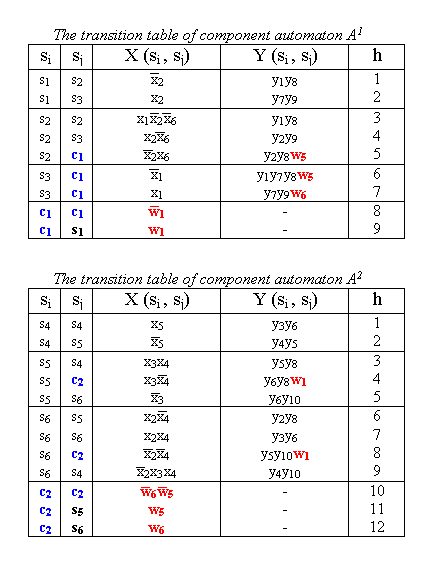
Also we can build transition tables of each component automaton:

Note: If there three or more signals in additional input (output) signals, then it is reasonable to code them by binary values. For example, to variables u₁ and u₂ are sufficient for coding four inputs w_i, w_j, w_k and . Also zero-number state (s₀) may be used to represent additional states (c_i)  in each of component automata.

Last update: 3 August, 2004